Parliament: A Threshold Secret Sharing Service

Written by Tobias Lauinger.

High-value secrets need proper protection. A well-established scheme to achieve this is secret sharing, which splits a secret into many parts and reveals nothing about the secret unless a quorum of shares is provided. This technique is used during key ceremonies. To secure a private key, the key is split and shares are distributed to several individuals. When the key is needed, all the individuals need to come together and provide their share. Depending on how often the secret needs to be accessed, the process of getting shareholders together can be costly and time consuming. It is also necessary to make sure the person who originally generates the shares, (and the person who combines the shares), does not retain a copy.

At Square, we protect signing keys, encryption keys, and other secrets with a secret sharing scheme. When access is requested, it is critical that shareholders can grant access to their share without them needing to be physically present — all the while maintaining a reasonable level of access control around the shares. For this reason we developed Parliament, a service that manages shares on the shareholder’s behalf.

Internally, Parliament uses Shamir’s threshold secret sharing scheme and encrypts every user’s shares under their public key. When shareholders decide to grant access to a secret, they submit their private key to Parliament and allow the service to temporarily decrypt their share and recompute the secret.

In the case of an attacker gaining temporary access to Parliament, only the secrets that are “unlocked” at the time of the attack are compromised. All other secrets remain confidential. In the following, we describe the cryptographic details of Parliament. Thank you to our advisor, Dan Boneh, for the useful insights and review of the protocol.

The Cryptography Behind Parliament

Parliament uses a threshold-based system where at least ( k ) out of ( n ) parts are required to reconstruct the original secret. Cryptographically, fewer than ( k ) parts combined reveal nothing about the secret; whereas the secret can be constructed deterministically from at least ( k ) parts. Parliament distributes shares so that at least ( k ) users need to give their approval before anyone can gain access to a secret. The threshold ( k ) can be set as a parameter when splitting a secret depending on the security requirements.

Arbitrary-Length Secret Sharing

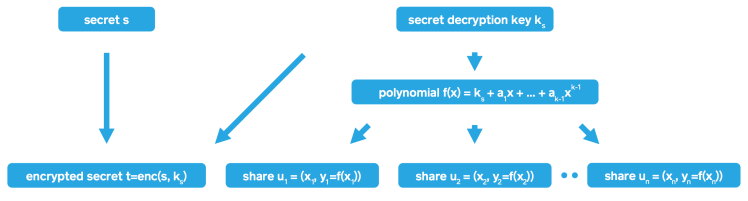
Parliament enables secret sharing of secrets with arbitrary lengths. Because computations for secret sharing require a prime modulus that is larger than the secret, (and it is preferable to use a fixed value for the prime modulus), Parliament implements arbitrary-length secret sharing on top of fixed-length secret sharing. In detail, Parliament first encrypts the secret ( s ) with a randomly generated symmetric key ( k_s ) (using AES256/GCM, which has a constant length). The result of this step is the encrypted secret ( t=enc(s, k_s) ) and the secret decryption key ( k_s ).

The secret decryption key ( k_s ) is then split into ( n ) shares using Shamir’s method and discarded afterwards. Shamir’s secret sharing involves generating a random polynomial ( f(x)=a_0+a_1x+a_2x^2+…+a_{k-1}x^{k-1} ) with ( a_0=k_s ), ( a_i \in [0; p-1] ) chosen at random for ( i=1, …, k-1 ), and ( p ) is prime. All computations involving the polynomial are made modulo ( p ) and the first coefficient corresponds to the secret decryption key. Because the length of ( k_s ) is 256 bits, the prime ( p ) is chosen to have an effective bit length of 257 bits so that ( 0 \le k_s < p ).

Each share ( u_j= (x_j, y_j=f(x_j)) ), ( j=1, …, n ) corresponds to a point on the polynomial curve, where any ( x_j ) can be public, but ( y_j ) should be kept secret by the owner of the share. There are multiple strategies to pick ( x_j ). We chose to draw ( x_j \in [0; p-1 ] ) at random in order to simplify the generation of additional shares at a later point in time. Sequence numbers or the hash of a user identifier are other conceivable values for ( x_j ), but such strategies would require bookkeeping of the highest assigned sequence number, or would not allow more than one share per user.

Arbitrary-Length Secret Sharing

Share Management

After the previous step, the initial secret sharing is complete with the encrypted secret ( t ) and the ( n ) shares ( u_j ) as the output. These shares can now be distributed to users, whose responsibility is to keep them secret. Of course, when access to the secret ( s ) is needed, users could choose to designate a trusted party that collects the shares and recombines them in order to gain access to the decryption key ( k_s ) and, eventually, decrypt the secret ( s ). However, this approach has several drawbacks, including (1) requiring users to manage their shares themselves; every time a new secret is added to the system or a secret sharing instance needs to be replaced, users would need to update their list of shares. And (2), every time a user is designated as the trusted party, that user is gaining access to the plaintext secret and could secretly keep a copy of it for unauthorised subsequent use.

To address these issues, we implemented Parliament to manage the shares on the shareholder’s behalf and store them in an encrypted way. We use public key cryptography so that Parliament can add shares by encrypting them with a user’s public key without the need for any user interaction. When a user, (in our case one of our security engineers), wishes to unlock a share to grant access to a secret, they provide Parliament with the corresponding private key. In principle, Parliament could have sent each share to its owner so that they decrypt it on their own, but this is impractical. As a security/usability trade-off, we decided that instead the user would send the secret key to Parliament and trust Parliament not to record the private key, decrypted share, or secret. That is, our design provides a reasonable protection against attackers with sporadic access to Parliament’s memory or database, but not against malicious code modification or administrators with permanent access to the machine running Parliament. This is not unlike the trust placed on the machine that combines the shares in any secret sharing algorithm.

Internally, the shares are encrypted using a hybrid encryption scheme: The secret share value ( y_j ) is encrypted with a randomly generated symmetric key ( k_{y_j} ) (using AES256/GCM): ( v_j=enc(y_j, k_{y_j}) ); the public value ( x_j ) remains unencrypted. The key ( k_{y_j} ) is then asymmetrically encrypted with the user’s public RSA key ( k_j^{pub} ) (using RSA2048/OAEP): ( w_j=enc(k_{y_j}, k_j^{pub}) ). In its database, Parliament stores the encrypted secret ( t ) along with a list of the users ( j ) holding a share of the corresponding decryption key, and for each user ( j ), Parliament stores the encrypted share ( v_j ) along with ( x_j ), the public part of the share, and the asymmetrically encrypted share decryption key ( w_j ).

Encryption of Shares

Granting Access to a Secret

When a user or an application requests access to a secret, Parliament will search its database to determine which users own a share and ask them to review the request. If a user approves, the user submits their private key to Parliament. Parliament decrypts the user’s share, caches it locally in volatile memory, and erases the user’s private key from memory. As soon as a threshold of ( k ) decrypted shares is reached, the authorised application can request the secret and Parliament will derive it from the decrypted shares. For security reasons, Parliament never caches the decrypted secret, but instead reconstructs it from the cached unencrypted shares. Also, requests for secrets time out after a configurable time interval, which will cause the corresponding unencrypted shares to be purged from memory.

In detail, when a user submits their private key ( k_j^{priv} ) to grant access to their share, Parliament uses it to decrypt the encrypted share decryption key ( w_j ) to obtain ( k_{y_j}=dec(w_j, k_j^{priv}) ) and then decrypts the secret share data ( y_j=dec(v_j, k_{y_j}) ). Once a threshold of at least ( k ) decrypted shares ( u_j=(x_j, y_j) ) has been reached, Parliament uses Lagrange interpolation to derive the secret sharing polynomial ( f(x) ) from the shares. The secret decryption key ( k_s ) corresponds to the value ( f(0) ), thus Parliament computes ( f(0)=\sum_{l=0}^{k-1} y_l \cdot \prod_{l \ne m} \frac{x_m}{x_m-x_l} = k_s ). With ( k_s ), Parliament decrypts the secret ( s=dec(t, k_s) ) and makes it available to the requesting application or user.

Operational Considerations

When a new user gains the right to grant access to a secret, an additional share needs to be generated for that user. It is possible to generate additional shares for an existing secret sharing instance by re-deriving the polynomial from the existing shares and evaluating the polynomial at a random point ( x’ ), as long as the threshold ( k ) remains the same. Changes to ( k ) require a new polynomial of higher or lower degree, thus new shares for all authorising users.

Under certain circumstances, shares need to be revoked. This can happen when a share has been disclosed, or when an employee is no longer authorised to approve requests for a given secret. In such a case, we generate a new secret sharing instance for the same secret and replace the old shares. Because we use a random symmetric key ( ( k_s ) ) to encrypt the secret to be shared, two successive invocations of the secret sharing procedure on the same secret will produce two sets of shares that are incompatible with each other. The encrypted secret ( t ) is replaced, too, which means that the old shares cannot be used any more to gain access to the secret ( s ), unless there exists a backup of ( t ). For this reason, high-value secrets may justify the additional effort of changing ( s ) altogether instead of changing only the shares.

There are a few attacks that Parliament does not defend against because we consider them out of scope. An attacker could replace each user’s public key with a value that is under the attacker’s control, and for which the corresponding private key is known to the attacker. When Parliament encrypts new shares with the attacker’s public key, the attacker can unlock all shares and gain access to the secret. Similarly, an attacker could replace all shares of a secret sharing instance with shares of another, possibly older and revoked instance, which would cause legitimate users of Parliament to use an outdated or incorrect secret. While the former attack could be devastating and leak secrets, the latter attack would most likely result in denial of service only. Both attacks require write access to the database. They highlight that in addition to a secure execution environment for the Parliament service, its database must be protected against unauthorised modifications, too. This assumption is common to many centralised services (such as LDAP) and we believe that it provides much better security than a decentralised approach with its usability issues and potentially lower adoption. Note that because we are using the Galois Counter Mode (GCM) when we symmetrically encrypt secrets, its built-in integrity check allows us to detect shares that do not belong to the same set, or shares that have been tampered with.

Conclusion

We implemented Parliament as a Java library using Bouncy Castle and BigInteger arithmetic, and on top of it a stand-alone command-line interface and a service interface. We are in the process of making the library and command-line interface available as open-source software.